The Tetragonal Crystal System

In the tetragonal system, like the orthorhombic system, the conventional unit cell is a parallelepiped, but two sides are equal, so that $a = b$ and $c \ne a$, while $\alpha = \beta = \gamma = \pi/2$, making this a special case of the orthorhombic system. The primitive vectors of the conventional unit cell are:
\[ \begin{array}{ccc} \mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \nonumber \\ \mathbf{a}_2 & = & a \, \mathbf{\hat{y}} \nonumber \\ \mathbf{a}_3 & = & c \, \mathbf{\hat{z}}. \end{array} \]
The volume of the conventional unit cell is \[ v = a^2 \, c . \]
Given the similarity between the tetragonal and orthorhombic crystal system, we might expect that the tetragonal system would have four bravais lattices as well, but the additional symmetry generated because $b = a$ reduces this to two. when $b \rightarrow a$, the base-centered orthorhombic bravais lattice becomes a simple tetragonal lattice, while the face-centered orthorhombic lattice can be shown to be identical to a body-centered tetragonal cell (see pgs. 115-117 of N. W. Ashcroft and N. D. Mermin, Solid State Physics).
Lattice 8: Simple Tetragonal

The simple tetragonal bravais lattice is identical to the conventional cell:
.\[ \begin{array}{ccc} \mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \nonumber \\ \mathbf{a}_2 & = & a \, \mathbf{\hat{y}} \nonumber \\ \mathbf{a}_3 & = & c \, \mathbf{\hat{z}}, \end{array} \]
with volume \[ v = a^2 \, c . \]
The space groups associated with the simple tetragonal lattice are:
\[ \begin{array}{lll} 75. ~ \text{P4} & 76. ~ \text{P4$_{1}$} & 77. ~ \text{P4$_{2}$} \\ 78. ~ \text{P4$_{3}$} & 81. ~ \text{P$\overline{4}$} & 83. ~ \text{P4/m} \\ 84. ~ \text{P4$_{2}$/m} & 85. ~ \text{P4/n} & 86. ~ \text{P4$_{2}$/n} \\ 89. ~ \text{P422} & 90. ~ \text{P42$_{1}$2} & 91. ~ \text{P4$_{1}$22} \\ 92. ~ \text{P4$_{1}$2$_{1}$2} & 93. ~ \text{P4$_{2}$22} & 94. ~ \text{P4$_{2}$2$_{1}$2} \\ 95. ~ \text{P4$_{3}$22} & 96. ~ \text{P4$_{3}$2$_{1}$2} & 99. ~ \text{P4mm} \\ 100. ~ \text{P4bm} & 101. ~ \text{P4$_{2}$cm} & 102. ~ \text{P4$_{2}$nm} \\ 103. ~ \text{P4cc} & 104. ~ \text{P4nc} & 105. ~ \text{P4$_{2}$mc} \\ 106. ~ \text{P4$_{2}$bc} & 111. ~ \text{P$\overline{4}$2m} & 112. ~ \text{P$\overline{4}$2c} \\ 113. ~ \text{P$\overline{4}$2$_{1}$m} & 114. ~ \text{P$\overline{4}$2$_{1}$c} & 115. ~ \text{P$\overline{4}$m2} \\ 116. ~ \text{P$\overline{4}$c2} & 117. ~ \text{P$\overline{4}$b2} & 118. ~ \text{P$\overline{4}$n2} \\ 123. ~ \text{P4/mmm} & 124. ~ \text{P4/mcc} & 125. ~ \text{P4/nbm} \\ 126. ~ \text{P4/nnc} & 127. ~ \text{P4/mbm} & 128. ~ \text{P4/mnc} \\ 129. ~ \text{P4/nmm} & 130. ~ \text{P4/ncc} & 131. ~ \text{P4$_{2}$/mmc} \\ 132. ~ \text{P4$_{2}$/mcm} & 133. ~ \text{P4$_{2}$/nbc} & 134. ~ \text{P4$_{2}$/nnm} \\ 135. ~ \text{P4$_{2}$/mbc} & 136. ~ \text{P4$_{2}$/mnm} & 137. ~ \text{P4$_{2}$/nmc} \\ 138. ~ \text{P4$_{2}$/ncm} & ~ & ~ \\ \end{array} \]
Lattice 9: Body-Centered Tetragonal
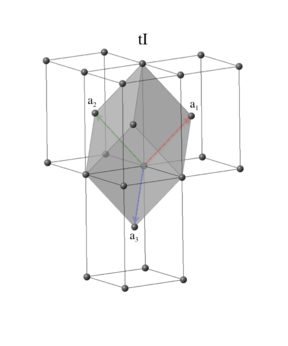
The body-centered tetragonal system has the same point group and translational symmetry as the simple tetragonal system, with the addition of a translation to the center of the parallelepiped. Our standard form of the primitive vectors is:
\[ \begin{array}{ccc} \mathbf{a}_1 & = & - \frac{a}{2} \, \mathbf{\hat{x}} + \frac{a}{2} \, \mathbf{\hat{y}} + \frac{c}{2} \, \mathbf{\hat{z}} \nonumber \\ \mathbf{a}_2 & = & ~ \frac{a}{2} \, \mathbf{\hat{x}} - \frac{a}{2} \, \mathbf{\hat{y}} + \frac{c}{2} \, \mathbf{\hat{z}} \nonumber \\ \mathbf{a}_3 & = & ~ \frac{a}{2} \, \mathbf{\hat{x}} + \frac{a}{2} \, \mathbf{\hat{y}} - \frac{c}{2} \, \mathbf{\hat{z}}. \end{array} \]
The volume of the primitive body-centered tetragonal unit cell is \[ v = \frac{a^2 \, c}{2}. \] There are two primitive body-centered tetragonal unit cells in the conventional tetragonal unit cell. The space groups associated with this lattice, all of which begin with $\text{I}$ in the standard notation, are:
\[ \begin{array}{lll} 79. ~ \text{I4} & 80. ~ \text{I4$_{1}$} & 82. ~ \text{I$\overline{4}$} \\ 87. ~ \text{I4/m} & 88. ~ \text{I4$_{1}$/a} & 97. ~ \text{I422} \\ 98. ~ \text{I4$_{1}$22} & 107. ~ \text{I4mm} & 108. ~ \text{I4cm} \\ 109. ~ \text{I4$_{1}$md} & 110. ~ \text{I4$_{1}$cd} & 119. ~ \text{I$\overline{4}$m2} \\ 120. ~ \text{I$\overline{4}$c2} & 121. ~ \text{I$\overline{4}$2m} & 122. ~ \text{I$\overline{4}$2d} \\ 139. ~ \text{I4/mmm} & 140. ~ \text{I4/mcm} & 141. ~ \text{I4$_{1}$/amd} \\ 142. ~ \text{I4$_{1}$/acd} & ~ & \\ \end{array} \]