The Orthorhombic Crystal System

In the orthorhombic system, the conventional unit cell is a parallelepiped defined by three mutually orthogonal vectors of unequal length: \[ \begin{array}{ccc} \mathbf{A}_1 & = & a \, \mathbf{\hat{x}} \nonumber \\ \mathbf{A}_2 & = & b \, \mathbf{\hat{y}} \nonumber \\ \mathbf{A}_3 & = & c \, \mathbf{\hat{z}}, \end{array} \] so that $a \ne b \ne c$, but $\alpha = \beta = \gamma = \pi/2$. It is a limiting case of the conventional monoclinic crystal with $\beta \rightarrow \pi/2$. The volume of the conventional unit cell is \[ V = a \, b \, c . \] There are four Bravais lattices in the orthorhombic system.
Lattice 4: Simple Orthorhombic
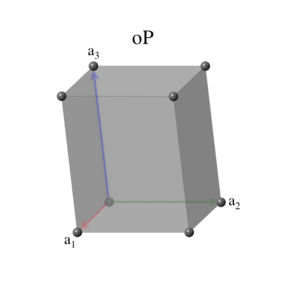
The simple orthorhombic Bravais lattice is identical to the conventional cell:
\[ \begin{array}{ccc} \mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \nonumber \\ \mathbf{a}_2 & = & b \, \mathbf{\hat{y}} \nonumber \\ \mathbf{a}_3 & = & c \, \mathbf{\hat{z}}, \end{array} \] with volume \[ V = a \, b \, c ~. \]
The space groups associated with the simple orthorhombic lattice are:
\[ \begin{array}{lll} 16. ~ \text{P222} & 17. ~ \text{P222$_{1}$} & 18. ~ \text{P2$_{1}$2$_{1}$2} \\ 19. ~ \text{P2$_{1}$2$_{1}$2$_{1}$} & 25. ~ \text{Pmm2} & 26. ~ \text{Pmc2$_{1}$} \\ 27. ~ \text{Pcc2} & 28. ~ \text{Pma2} & 29. ~ \text{Pca2$_{1}$} \\ 30. ~ \text{Pnc2} & 31. ~ \text{Pmn2$_{1}$} & 32. ~ \text{Pba2} \\ 33. ~ \text{Pna2$_{1}$} & 34. ~ \text{Pnn2} & 47. ~ \text{Pmmm} \\ 48. ~ \text{Pnnn} & 49. ~ \text{Pccm} & 50. ~ \text{Pban} \\ 51. ~ \text{Pmma} & 52. ~ \text{Pnna} & 53. ~ \text{Pmna} \\ 54. ~ \text{Pcca} & 55. ~ \text{Pbam} & 56. ~ \text{Pccn} \\ 57. ~ \text{Pbcm} & 58. ~ \text{Pnnm} & 59. ~ \text{Pmmn} \\ 60. ~ \text{Pbcn} & 61. ~ \text{Pbca} & 62. ~ \text{Pnma} \\ \end{array} \]
Lattice 5: Base-Centered Orthorhombic
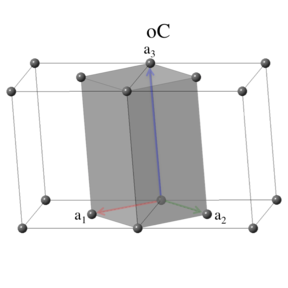
Like the base-centered monoclinic lattice, the base-centered orthorhombic system allows a translation in one of the base planes. Unfortunately, the standard plane chosen depends on the space group, as shown in the table below. Space groups beginning with C put the translation in the $a-b$ plane, that is, the plane defined by $\mathbf{A}_1$ and $\mathbf{A}_2$. In this case the primitive vectors can be taken to be
\[ \begin{array}{ccc} \mathbf{a}_1 & = & \frac{a}{2} \, \mathbf{\hat{x}} - \frac{b}{2} \, \mathbf{\hat{y}} \nonumber \\ \mathbf{a}_2 & = & \frac{a}{2} \, \mathbf{\hat{x}} + \frac{b}{2} \, \mathbf{\hat{y}} \nonumber \\ \mathbf{a}_3 & = & c \, \mathbf{\hat{z}} ~. \end{array} \]
Space groups beginning with A put the translation in the $b-c$ plane, defined by $\mathbf{A}_2$ and $\mathbf{A}_3$. We use the primitive vectors
\[ \begin{array}{ccc} \mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \nonumber \\ \mathbf{a}_2 & = & \frac{b}{2} \, \mathbf{\hat{y}} - \frac{c}{2} \, \mathbf{\hat{z}} \nonumber \\ \mathbf{a}_3 & = & \frac{b}{2} \, \mathbf{\hat{y}} + \frac{c}{2} \, \mathbf{\hat{z}}. \end{array} \]
The above orientation is not the one used
by Setyawan
and Curtarolo who only considered centering in
the C
plane defined by $\mathbf{a}_2$ and
$\mathbf{a}_3$. A simple rotation brings the vectors into
agreement. In both cases the volume of the primitive unit
cell is \[ V = \frac{a \, b \, c}{2}. \]
There are two primitive base-centered orthorhombic unit cells in the conventional orthorhombic unit cell. The space groups associated with the base-centered orthorhombic lattice are
\[ \begin{array}{lll} 20. ~ \text{C222$_{1}$} & 21. ~ \text{C222} & 35. ~ \text{Cmm2} \\ 36. ~ \text{Cmc2$_{1}$} & 37. ~ \text{Ccc2} & 38. ~ \text{Amm2} \\ 39. ~ \text{Abm2} & 40. ~ \text{Ama2} & 41. ~ \text{Aba2} \\ 63. ~ \text{Cmcm} & 64. ~ \text{Cmca} & 65. ~ \text{Cmmm} \\ 66. ~ \text{Cccm} & 67. ~ \text{Cmma} & 68. ~ \text{Ccca} \\ \end{array} \]
Lattice 6: Body-Centered Orthorhombic
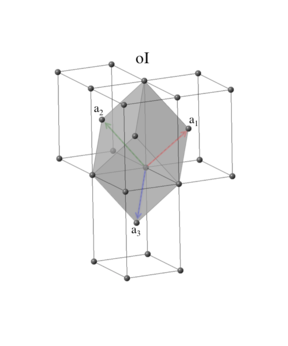
The body-centered orthorhombic lattice has the same point group and translational symmetry as the simple orthorhombic system, with the addition of a translation to the center of the parallelepiped. Our standard form for the primitive vectors is
\[ \begin{array}{ccc} \mathbf{a}_1 & = & - \frac{a}{2} \, \mathbf{\hat{x}} + \frac{b}{2} \, \mathbf{\hat{y}} + \frac{c}{2} \, \mathbf{\hat{z}} \nonumber \\ \mathbf{a}_2 & = & ~ \frac{a}{2} \, \mathbf{\hat{x}} - \frac{b}{2} \, \mathbf{\hat{y}} + \frac{c}{2} \, \mathbf{\hat{z}} \nonumber \\ \mathbf{a}_3 & = & ~ \frac{a}{2} \, \mathbf{\hat{x}} + \frac{b}{2} \, \mathbf{\hat{y}} - \frac{c}{2} \, \mathbf{\hat{z}}. \end{array} \]
The volume of the primitive body-centered orthorhombic unit cell is \[ V = \frac{a \, b \, c}{2}. \] There are two primitive body-centered orthorhombic unit cells in the conventional orthorhombic unit cell. The space groups associated with this lattice, all of which begin with $\text{I}$ in the standard notation, are
\[ \begin{array}{lll} 23. ~ \text{I222} & 24. ~ \text{I2$_{1}$2$_{1}$2$_{1}$} & 44. ~ \text{Imm2} \\ 45. ~ \text{Iba2} & 46. ~ \text{Ima2} & 71. ~ \text{Immm} \\ 72. ~ \text{Ibam} & 73. ~ \text{Ibca} & 74. ~ \text{Imma} \\ \end{array} \]
Lattice 7: Face-Centered Orthorhombic
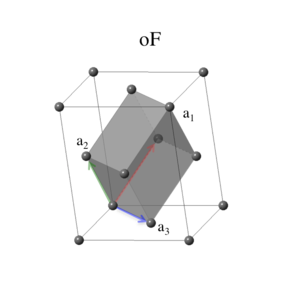
While the base-centered monoclinic lattice allows translations to one base plane, the face-centered orthorhombic lattice allows translations to any of the base planes. Our standard choice for the primitive vectors of this system are given by
\[ \begin{array}{ccc} \mathbf{a}_1 & = & ~ \frac{b}{2} \, \mathbf{\hat{y}} + \frac{c}{2} \, \mathbf{\hat{z}} \\ \mathbf{a}_2 & = & ~ \frac{a}{2} \, \mathbf{\hat{x}} + \frac{c}{2} \, \mathbf{\hat{z}} \\ \mathbf{a}_3 & = & ~ \frac{a}{2} \, \mathbf{\hat{x}} + \frac{b}{2} \, \mathbf{\hat{y}}. \end{array} \]
The volume of the primitive face-centered orthorhombic unit cell is \[ V = \frac{a \, b \, c}{4}~\], puting are four primitive body-centered orthorhombic unit cells into the conventional orthorhombic unit cell. The space groups associated with this lattice, all of which begin with $\text{F}$ in standard notation, are
\[ \begin{array}{lll} 22. ~ \text{F222} & 42. ~ \text{Fmm2} & 43. ~ \text{Fdd2} \\ 69. ~ \text{Fmmm} & 70. ~ \text{Fddd} & \\ \end{array} \]